Load Flow Analysis Using Newton-Raphson and Gauss-Seidel Methods

Load flow analysis, also known as power flow analysis, is an essential task in power system studies. It determines the steady-state voltages, real and reactive power flows, and power losses in a power network under normal operating conditions. It is vital for:

• Designing future expansion

• Optimizing existing networks

• Real-time monitoring

• Planning contingencies

The load flow problem is inherently non-linear, and its solution requires iterative numerical methods. Among the most commonly used techniques are:

• Gauss-Seidel Method

• Newton-Raphson Method

This article will cover both these methods in detail, explain their differences, and discuss where and when to use them.

1. Power Flow Problem Formulation

For a power system with n buses, we categorize buses as:

• Slack Bus: Voltage magnitude and angle are specified (reference bus).

• PV Bus: Real power and voltage magnitude are specified.

• PQ Bus: Real and reactive powers are specified.

The power flow equations for bus i are:

$$P_i = \sum_{j=1}^{n} |V_i||V_j||Y_{ij}|\cos(\theta_{ij} + \delta_j - \delta_i)$$ $$Q_i = \sum_{j=1}^{n} |V_i||V_j||Y_{ij}|\sin(\theta_{ij} + \delta_j - \delta_i)$$

Where:

• $V_i, V_j$: Voltages at buses i and j

• $Y_{ij}$: Element of the admittance matrix

• $\delta_i, \delta_j$: Voltage angles

• $\theta_{ij}$: Angle of admittance

These equations are non-linear and are solved using iterative techniques.

2. Gauss-Seidel Method

Overview

The Gauss-Seidel method is an extension of the classical technique used for solving linear equations. It updates bus voltages sequentially and uses the latest values during the iteration.

Steps

1. Initialize voltages for all buses (usually 1∠0° p.u.).

2. Update each PQ bus voltage using:

   $$V_i^{(k+1)} = \frac{1}{Y_{ii}} \left[ \frac{P_i - jQ_i}{(V_i^{(k)})^*} - \sum_{j=1, j\neq i}^{n} Y_{ij} V_j^{(k+1)} \right]$$

3. Continue iterations until convergence is achieved (voltage change below tolerance).

Advantages

• Simple to understand and implement.

• Low memory requirement.

Disadvantages

• Slow convergence, especially for large systems.

• Sensitive to initial guess and ordering.

3. Newton-Raphson Method

Overview

The Newton-Raphson method uses a Taylor series expansion and Jacobian matrix to solve the power flow equations. It’s more mathematically intensive but offers faster and more reliable convergence.

Steps

1. Formulate a set of non-linear equations:

   $$\mathbf{f}(x) = 0$$

   Where $x = [\delta_2, ..., \delta_n, V_{m+1}, ..., V_n]$ is the state vector.

2. Perform Taylor series expansion:

   $$\mathbf{f}(x + \Delta x) \approx \mathbf{f}(x) + J(x) \Delta x = 0 \Rightarrow \Delta x = -J(x)^{-1} \mathbf{f}(x)$$

3. Solve linear system for Δx and update state variables.

4. Iterate until $|\Delta x|$ is less than specified tolerance.

Jacobian Matrix Structure

$$J = \begin{bmatrix} \frac{\partial P}{\partial \delta} & \frac{\partial P}{\partial V} \\ \frac{\partial Q}{\partial \delta} & \frac{\partial Q}{\partial V} \end{bmatrix}$$

Advantages

• Fast convergence, typically within 3–6 iterations.

• Less sensitive to system size and initial guesses.

Disadvantages

• Requires more memory and computational power.

• More complex to program.

4. Comparison: Gauss-Seidel vs Newton-Raphson

Feature	Gauss-Seidel	Newton-Raphson
Convergence Speed	Slow	Fast
Complexity	Low	High
Memory Requirement	Low	High
Sensitivity	High (initial guess, size)	Low
Preferred For	Small systems	Large and complex systems

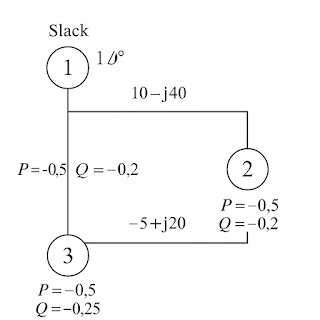
5. Numerical Example (Simplified)

Assume a 3-bus system:

• Bus 1: Slack (1∠0°)

• Bus 2: PQ (P = -0.5, Q = -0.2)

• Bus 3: PQ (P = -0.6, Q = -0.25)

Y-Bus matrix:

$$Y = \begin{bmatrix} 10 - j40 & -5 + j20 & -5 + j20 \\ -5 + j20 & 10 - j40 & -5 + j20 \\ -5 + j20 & -5 + j20 & 10 - j40 \\ \end{bmatrix}$$

Using either method, we solve for voltage magnitude and angles at Bus 2 and 3. Newton-Raphson would converge in ~3–4 iterations, while Gauss-Seidel may require 15+.

(For actual computation steps, a simulation or detailed walkthrough with complex arithmetic is ideal.)

FAQs

Q1: Why is load flow analysis important?

A: It helps engineers plan, operate, and expand the power system reliably by determining power flows, voltages, and losses.

Q2: Which method should I use for a large power system?

A: The Newton-Raphson method is preferred for large and complex systems due to its fast convergence and robustness.

Q3: Can Gauss-Seidel method be used in real-time applications?

A: Not ideally. It is slow and less stable compared to Newton-Raphson, making it unsuitable for real-time operations.

Q4: What are typical convergence criteria?

A: A common criterion is when the change in bus voltage magnitude or angle is less than $10^{-4}$ per unit or radians.

Q5: Are there other methods besides these two?

A: Yes, alternatives include:

• Fast Decoupled Load Flow (FDLF)

• Modified Newton-Raphson

• DC Load Flow (approximate method)

Conclusion

Load flow analysis is a cornerstone of power system engineering. Both Gauss-Seidel and Newton-Raphson methods have their place in power system studies. While Gauss-Seidel is educational and easy to code, Newton-Raphson stands out in real-world power systems due to its efficiency and reliability.

For practical applications, especially in modern high-voltage networks, Newton-Raphson is the method of choice.